Approfondissons un peu plus en détail les notions de « représentation de formes géométriques » pour mieux comprendre le concept d’image vectorielle ou de dessin vectoriel interprété ou représenté par exemple dans Illustrator, Autocad, Maya, 3DSMax.
Comme vu dans le cours sur les bases du dessin vectoriel, une image vectorielle est formée d’un assemblage d’une ou plusieurs formes géométriques (formes vectorielles ou objets vectoriels).
- | Voir : Les bases du dessin vectoriel |
Que veut dire : Composé d’un assemblage d’une ou plusieurs formes géométriques ?
Prenons une feuille de papier quadriller (une feuille de papier millimétré par exemple) et traçons-y un carré en respectant la technique du point et de la ligne droite reliant les points.
Nous obtenons donc pour représenter ce carré 4 points (nommé pour l’exemple A – B – C – D) et 4 lignes droites.
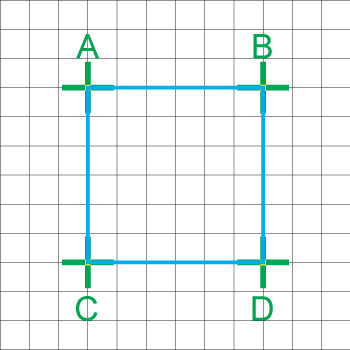
- On trace des lignes droites reliant les points A – B – C – D pour former le carré
Que déduit-on de l’observation du tracé géométrique du carré ?
- Pour pouvoir représenter un carré sur notre feuille, la première chose à faire est de tracer les 4 points (A – B – C – D) qui permettent ensuite son tracé.
- Notre carré représenté sur notre feuille est composé de 4 lignes droites, soit dit autrement composé de 4 formes géométriques (Rmq : la lignes droite étant une forme géométrique).
- Notre carré sur notre feuille a une position bien précise (il est au centre de la feuille pour notre exemple). La position des 4 points qui le composent (A – B – C – D) est donc importante.
De ces points d’observation, on en tire les grands principes de la compréhension, l’utilisation et la maîtrise de la technique du dessin vectoriel.
Les objets vectoriels
Les formes géométriques obtenues dans un logiciel de dessin vectoriel sont appelées objets vectoriels.
Le tracé et les points d’ancrage
Les objets vectoriels sont composés d’un tracé (« squelette » de la forme) articulé autour/par des points clés appelés points d’ancrage.
Les points d’ancrage déterminent le début et la fin d’une forme vectorielle (objet vectoriel) mais aussi les points de tensions, de flexion etc., de la forme géométrique que l’on veut réaliser.
Si l’on reprend notre exemple du carré :
- Les points d’ancrage sont les 4 points : A – B – C – D
- Le tracé est : la ligne tracée entre les 4 points
Exemple de points d’ancrage pour un cercle ou une ellipse
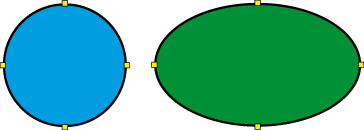
- Lignes noires = Tracé de la forme (objet vectoriel)
Points jaunes = Points d’ancrage de la forme (objet vectoriel)
Exemple de points d’ancrage d’une forme géométrique quelconque (objet vectoriel quelconque)
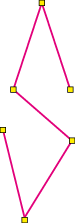
- Lignes rouges = Tracé de la forme (objet vectoriel)
Points jaunes = Points d’ancrage de la forme (objet vectoriel)
Le cadre de sélection (encapsulage de la forme géométrique)
Dans les programmes de dessin vectoriel, pour déplacer l’objet vectoriel (la forme vectorielle) dans son ensemble c’est à dire déplacer le tracé de l’objet et de l’ensemble de ses points d’ancrage, l’objet vectoriel est alors « encapsulé » dans sa globalité dans un conteneur appelé cadre de sélection.
Le cadre de sélection permet ainsi de sélectionner l’objet (tracé et points d’ancrage) et permet ainsi de le modifier, le déplacer, … dans son ensemble.
Quel que soit la complexité de l’objet vectoriel (forme vectorielle) obtenu, celui-ci peut toujours être contenu dans cadre de sélection de forme quadrilatère : le « carré » ou « rectangle » (le rectangle étant un carré étiré), pour les dessins en 2 dimensions.
Pour notre exemple du carré, son cadre de sélection est de même forme que l’objet vectoriel, mais si on prend l’exemple d’un cercle son cadre de sélection est quant à lui carré. Pour une ellipse son cadre de sélection sera quant à lui rectangulaire.
Nous verrons de nombreux avantages de cet encapsulage d’un objet vectoriel dans ce que l’on appelle un cadre de sélection par la suite.
Pour notre cercle et notre ellipse :
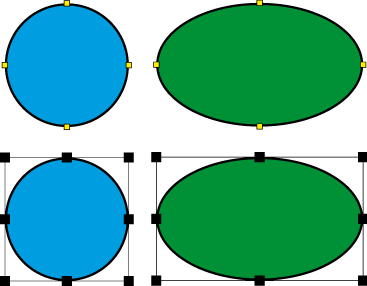
- Lignes noires = Tracé de la forme (objet vectoriel)
Points jaunes = Points d’ancrage de la forme (objet vectoriel)
Points noirs + lignes noires autour de l’objet vectoriel = cadre de sélection de la forme (objet vectoriel)
Pour notre forme quelconque :
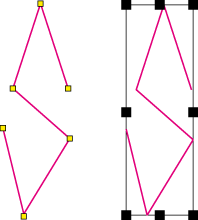
- Lignes rouges = Tracé de la forme (objet vectoriel)
Points jaunes = Points d’ancrage de la forme (objet vectoriel)
Points noirs + lignes noires autour de l’objet vectoriel = cadre de sélection de la forme (objet vectoriel)
Mémorisation des objets vectoriels d’une image vectorielle
Objet(s) vectoriel(s) et image vectorielle
Chaque objet vectoriel composant l’image vectorielle est mémorisé sur le support d’enregistrement (disque dur, …) sous forme d’expression « mathématique ».
Contrairement aux images matricielles (| Voir : les images matricielles |) ou il faut mémoriser chaque pixel composant l’image, là tous les objets vectoriels sont mémorisés sous forme de formule(s) mathématique(s), ce qui permet ainsi d’obtenir des fichiers très léger, mais surtout ce qui permet d’agrandir ou de rétrécir les objets à l’écran sans altération de qualité (Rmq : il n’y a pas comme avec les images matricielles d’effet escalier).
Pour bien comprendre prenons l’exemple d’une ligne droite (cela pourrait être une ligne composant une partie du tracé du carré précédemment étudié).
Pour mémoriser les informations de cette ligne sous forme d’objet vectoriel (donc sous forme de tracé et points d’ancrages) on peut imaginer que celle-ci soit simplement ramenée à une simple formule mathématique ayant pour base l’expression : y = x.
A savoir : L’ensemble des objets vectoriels enregistrés et composant notre création est appelé image vectorielle.
Dit autrement : une image vectorielle est composée d’un ou plusieurs objets vectoriels.
Comparaison de l’enregistrement d’une image vectorielle et d’une image matricielle
L’enregistrement d’une image vectorielle
Symboliquement, une image vectorielle est enregistrée différemment de sa projection sur un écran, l’image vectorielle est enregistrée sous forme d’expression(s) mathématique(s).
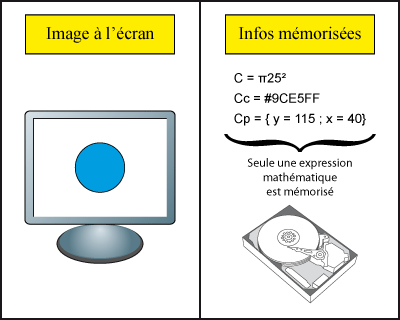
- Image vectorielle => Cercle bleu à l’écran / Une expression mathématique définissant le cercle bleu est enregistrée
Rmq : L’image vectorielle ici n’est composé que d’un objet vectoriel (un cercle bleu)
L’enregistrement d’une image matricielle
Symboliquement, une image matricielle est enregistrée de façon identique à son affichage écran, chaque pixel composant l’image matricielle est enregistré comme projeté à l’écran.
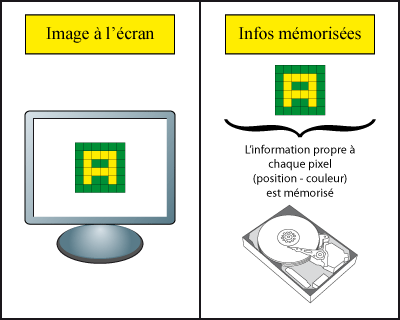
- Image matricielle => lettre « A » à l’écran / l’information de chaque pixel est mémorisée
En conclusion : la mémorisation d’une image vectorielle n’est donc pas la même que la mémorisation d’une image matricielle.
Avantages des images vectorielles
Les objets vectoriels constituant l’image vectorielle mémorisées (ou stockées) sous forme d »expressions mathématiques sur notre support numérique (disque dur, clé USB etc.) ne prennent que très peu de place.
Rmq : une formule telle que y = ax+b est beaucoup plus légère à mémoriser qu’une multitude de points (pixels) composant une ligne droite dans la technique des images matricielles.
Comme les images vectorielles sont composés de formes géométriques (objets vectoriels) elles-mêmes obtenues par des formules mathématiques, ces images peuvent donc être agrandis ou diminués par calcul (en agissant sur les formules directement) et ne subissent donc pas d’altérations (effet escalier) lors de leur affichage sur un écran.
- | Voir : les images vectorielles et matricielles |
On peut aussi dire « symboliquement » que les « dessins vectoriels » ou images vectorielles n’ont pas de dimensions réelles mais s’adaptent à notre besoin.
Un exemple pour bien comprendre la spécificité d’une image vectorielle par rapport à une image matricielle :
Si l’on reprend l’exemple du cercle, dans le cas d’une image vectorielle, si l’on décide de le diminuer, nous n’avons qu’à agir sur la ou les formules mathématiques qui le constituent, en l’occurrence nous n’avons qu’à agir sur la taille du rayon du cercle.
Par contre si maintenant ce même cercle est représenté par une image matricielle, si l’on veut diminuer la taille de cette image comment puis-je m’y prendre ?
Comment puis-je enlever des pixels à mon image, et lesquels ?
Toute une série de questions qui deviennent beaucoup plus complexes à gérer et qui n’existent pas quand on travaille avec un outil vectoriel.

- On peut observer que seul le rayon du cercle est changé si l’on augmente ou diminue la taille de l’objet vectoriel, l’image vectorielle n’est ainsi pas détériorée à l’écran
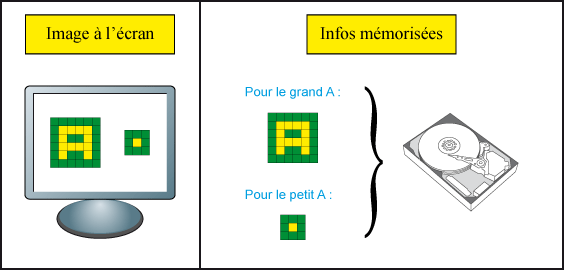
- On peut observer que si l’on diminue la taille de l’image matricielle (avec un programme de retouche d’image et des paramètres classiques), le nombre de pixels constituant l’image matricielle a diminué, et donc l’affichage de l’image matricielle s’est détérioré
Rmq : Des préjugés existent sur le fait de la qualité des images obtenues de façon vectorielle ne peuvent pas être aussi réalistes que des images matricielles.
Il ne dépend que de l’artiste d’atteindre ce même réalisme et non de l’outil employé.
Une petite fouille sur Internet permet de se ramener à une réalité.
Souvent une non connaissance des outils vectoriels nous laisse à penser cela. N’oublions pas que la 3D est bâtie sur ces principes et qu’aujourd’hui on s’en sert beaucoup pour créer des images de décors de cinéma que l’on incruste dans des films.
Positionnement des objets vectoriels
Repère orthonormé (coordonnées X, Y ou X, Y, Z)
Pour définir la position d’un objet vectoriel (forme vectorielle ou dessin vectoriel) sur notre écran, il faut définir une position des points d’ancrage qui le composent.
Il en découle donc la notion de repère orthonormé (rappelez-vous vos anciens cours de mathématique quand il fallait prendre ses doigts pour les imaginer…) qui nous permettent ainsi de définir l’emplacement de ces points d’ancrage par des coordonnées.
- Cordonnées X et Y s’il s’agit d’image vectorielle 2D (dans Illustrator par exemple)
- Cordonnées X, Y, Z pour les images vectorielles en 3D (dans Maya, 3DSMax, …)
Rappel au passage : les bases acquises sur le dessin vectoriel sont les mêmes pour les images 2D que 3D ! Vous ne perdez donc vraiment pas votre temps à lire tout cela ! De plus avec les versions dernières versions d’Illustrator, des « effets » 3D sont possibles !
En conclusion : pour représenter toute forme dans un programme de dessin vectoriel tel qu’Illustrator, Autocad, Maya, … nous auront forcément un repère orthonormé implicite.
- Repères orthonormés X, Y et Repères orthonormés X, Y, Z
Synthèse des points et vocabulaire à connaitre pour Illustrator
- Une image vectorielle est composée d’un ou plusieurs objets vectoriels
- Chaque objet vectoriel est composé d’un tracé et de points d’ancrage (rmq : au tracé ou peut lui appliquer un contour !)
- Chaque objet vectoriel ou ensemble d’objets vectoriels lors d’une sélection est encapsulé dans un cadre de sélection
- La dimension (la taille) des objets vectoriels ou images vectorielles peuvent s’adapter aux besoins sans altération
- Chaque objet vectoriel ou groupe d’objets vectoriels est positionné selon un repère orthonormé de coordonnées x, y
- Le poids (le volume) des fichiers vectoriels (images vectorielles) est généralement nettement moins volumineux qu’une même image sous forme matricielle de haute définition
Une fois ses principes bien compris et assimilés, la suite va en découler et donc va être facilement compréhensible (parfois il faut relire plusieurs fois ces explications).
Vous allez maintenant avec ces quelques principes connus gagner énormément de temps !
Bien sûr le talent du dessinateur n’a rien avoir avec ces connaissances, mais pour lui permettre de réaliser ce qu’il souhaite avec un outil vectoriel, l’artiste ne peut se passer de ces bases.
Maintenant ouvrez votre programme Illustrator et commencez !
